Solar & Stellar Astrophysics

Expanding solar braiding models to explain different flare frequency distributions in other stars.

We expanded upon a theoretical model in which coronal magnetic fields braid and reconnect to produce a shallower distribution of flare energies in stars that rotate more rapidly (corresponding to a weaker decline in occurrence rates toward increasing flare energies), and tentative evidence for the predicted rotation-power-law index correlation in TESS observations of flaring events.

Want to read more? Check out our manuscript here: Seligman, Rogers, Feinstein, et al. 2022, ApJ, 929, 54.

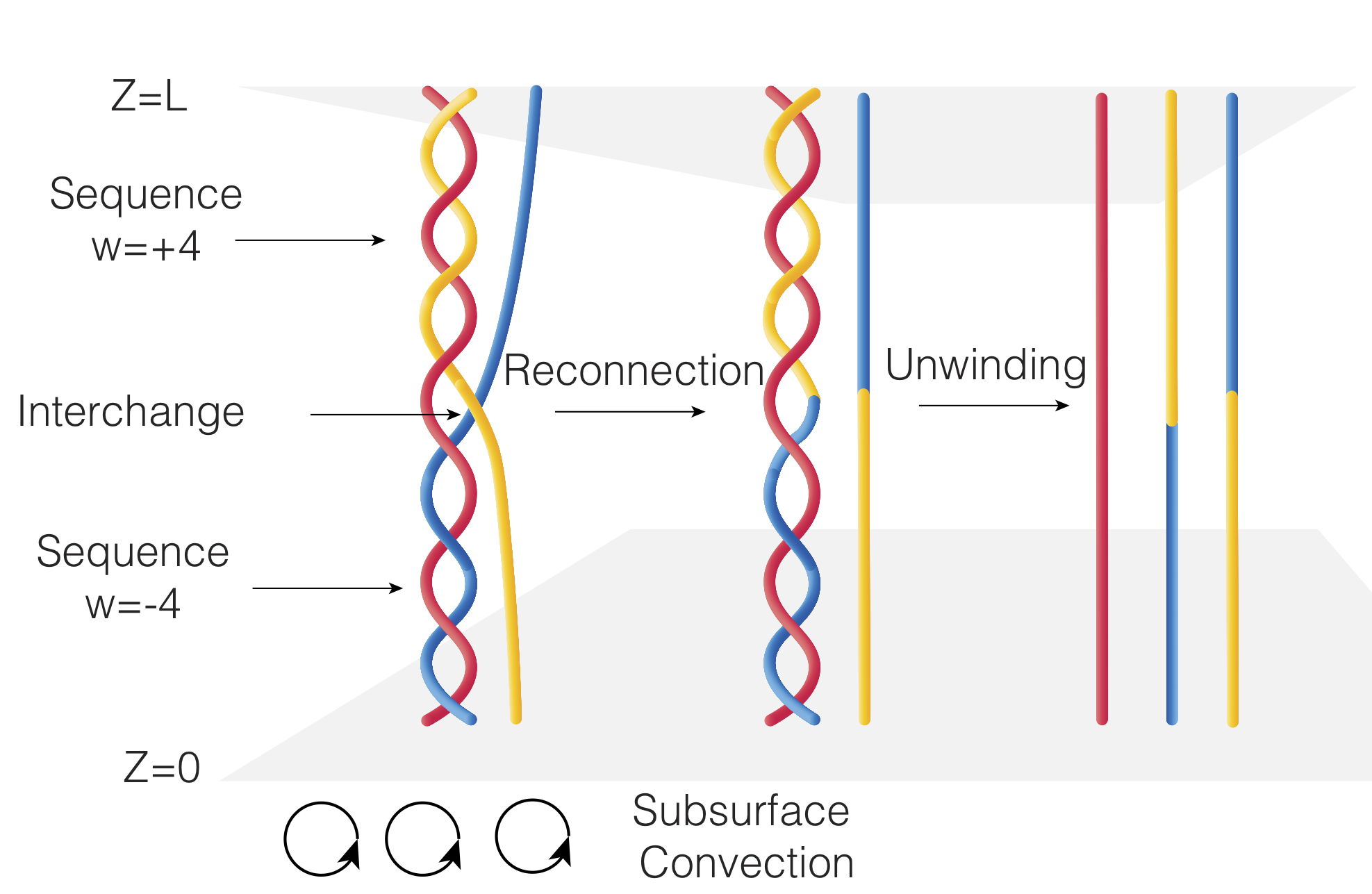
Constraining theoretical models of energy transport mechanisms in the Sun.

We compared the average photospheric current helicity Hc, photospheric twist parameter α (a well-known proxy for the full relative magnetic helicity), and subsurface kinetic helicity Hk for 194 active regions observed between 2006–2013. We use 2440 Hinode photospheric vector magnetograms, and the corresponding subsurface fluid velocity data derived from GONG (2006–2012) and Helioseismic and Magnetic Imager (2010–2013) dopplergrams. We found a significant hemispheric bias in all three parameters. Subsurface fluid motions of a given handedness correspond to photospheric helicities of both signs in approximately equal numbers. However, common variations appeared in annual averages of these quantities over all regions. Furthermore, in a subset of 77 regions, we found significant correlations between the temporal profiles of the subsurface and photospheric helicities. In these cases, the sign of the linear correlation coefficient matched the sign relationship between the helicities, indicating that the photospheric magnetic field twist was sensitive to the twisting motions below the surface.

Want to read more? Check out our manuscript here: Seligman, Petrie, & Komm, 2014, ApJ, 795, 113.

Stellar coronae exist in a self-organized critical state.

The theory of self-organized criticality describes a class of dissipative dynamical systems which remain at a critical point with no intrinsic length or time scale. The existence of the critical state requires a local instability, which occurs when some parameter exceeds its critical value and results in a dissipative transport process where this same parameter increases at neighboring sites. A simple physical analogy is a sand pile. As sand particles are added, the difference in height between neighboring sites on the pile increases. When the additional sand particles make the new height difference exceed a critical threshold, avalanche events occur. This system maintains a critical slope, representing a dynamical attractor that is insensitive to the initial conditions. This critical state is maintained via nonlinear avalanche events spanning all length scales triggered by perturbations.

Want to read more? Check out our manuscript here: Feinstein, Seligman, Günther, & Adams, 2022, ApJL, 925, L9.